이론정리

  • Statinary Data (정상 데이터) : 시간의 흐름에 따라 평균과 분산이 일정

  • Nonstationary Process(비정상 프로세스) : 시간의 흐름에 따라 평균과 분산이 변경됨 ( ex: 주가)

    ACF를 보면 천천히 줄어드는 그래프의 형태를 띰.

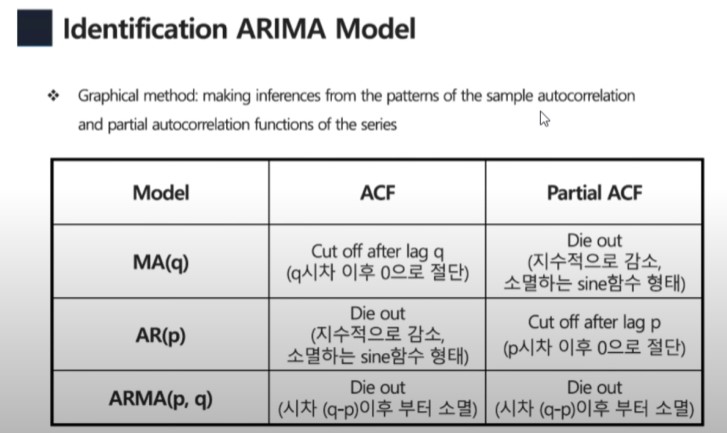
  • Autocorrelation

    Autocorrelation lag 1 : 자기 자신과 1시점 이후 data와의 correlation (lag 2의 경우 2시점 이후 data와 비교)

  • Partial Autocorrelation

  • Autoregressive (AR) Models

    • 예측시점의 값을 구할 때 과거의 data들(과거의 y값)을 활용하여 y값을 구함.(lag 변수 활용)

    • 에러를 구할 때, 최소제곱법을 활용할 수는 없음.

  • Moving Average (MA) Models

    • 예측시점의 Error를 과거 Error를 활용하여 예측.

  • Autoregressive and Moving Average (ARMA)

    • 예측시점의 값을 과거의 lag 값과 Error를 활용하여 예측.

  • AR/MA/ARMA의 경우 Data가 Stationary여야함.

  • Autoregressive Integrated Moving Average (ARIMA)

    • Differencing을 통해 Non-stationary data를 Stationary로 만들고 예측함. ( I (integrated) = differencing 횟수)

      • Differencing (차분) : 현 시점 데이터에서 d시점 이전 데이터를 뺀 것.

      • 일반 적인 데이터는 1차 차분만으로 stationary가됨. 2차 차분을 넘어서야 stationary가 되는 data는 ARIMA를 사용하기에 적합하지 않음.

    • (p,d,q)를 이용하여 모델을 구성. (ex : 0,1,1 -> Differencing을 한 번 한 MA 모델)

    • p : AR 모델의 Independent variable의 개수.(시점의 개수) (order of the AR part of the model)

    • d : differencing. (order of differencing)

    • q : error의 개수. (order of the MA part of the model)

  • AIC를 계산하여 AIC가 작은 Model을 선정. s

from PIL import Image
Image.open('Identification ARIMA Model.jpg')

Identification ARIMA Model

Passenger Data 예제

import os

import pandas as pd
import pandas_datareader.data as pdr

from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score

import matplotlib.pyplot as plt
import matplotlib
plt.style.use('seaborn-whitegrid')

import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
from pmdarima.arima import auto_arima

import seaborn as sns

plt.style.use('seaborn-whitegrid')
%matplotlib inline

import itertools

import warnings
warnings.filterwarnings('ignore')

data = pd.read_csv('AirPassengers.csv')
data = data.rename(columns={'Month':'month', '#Passengers':'passengers'})
data['month'] = pd.to_datetime(data['month'])
data = data.set_index('month')
data
passengers
month
1949-01-01 112
1949-02-01 118
1949-03-01 132
1949-04-01 129
1949-05-01 121
... ...
1960-08-01 606
1960-09-01 508
1960-10-01 461
1960-11-01 390
1960-12-01 432

144 rows × 1 columns

Data Preprocessing

# Raw data plot
fig = data.plot()


decomposition = sm.tsa.seasonal_decompose(data['passengers'], model='additive', period=1)
fig = decomposition.plot()
fig.set_size_inches(10,10)
plt.show()

Identify Model to be Tentatively Entertainted

train_data, test_data = train_test_split(data, test_size=0.2, shuffle=False)

# ACF, PACF plot

# https://www.statsmodels.org/stable/generated/statsmodels.graphics.tsaplots.plot_acf.html
# https://www.statsmodels.org/stable/generated/statsmodels.graphics.tsaplots.plot_pacf.html

fig,ax = plt.subplots(1,2,figsize=(10,5))
fig.suptitle('RawData')
sm.graphics.tsa.plot_acf(train_data.values.squeeze(), lags=30, ax=ax[0])
sm.graphics.tsa.plot_pacf(train_data.values.squeeze(), lags=30, ax=ax[1]);

Differencing

diff_train_data = train_data.copy()
diff_train_data = diff_train_data['passengers'].diff()
diff_train_data = diff_train_data.dropna()
print('###### Raw Data ######')
print(train_data)
print('### Differenced Data ###')
print(diff_train_data)

###### Raw Data ######
            passengers
month                 
1949-01-01         112
1949-02-01         118
1949-03-01         132
1949-04-01         129
1949-05-01         121
...                ...
1958-03-01         362
1958-04-01         348
1958-05-01         363
1958-06-01         435
1958-07-01         491

[115 rows x 1 columns]
### Differenced Data ###
month
1949-02-01     6.0
1949-03-01    14.0
1949-04-01    -3.0
1949-05-01    -8.0
1949-06-01    14.0
              ... 
1958-03-01    44.0
1958-04-01   -14.0
1958-05-01    15.0
1958-06-01    72.0
1958-07-01    56.0
Name: passengers, Length: 114, dtype: float64

# Differenced data plot

plt.figure(figsize=(12,8))
plt.subplot(211)
plt.plot(train_data['passengers'])
plt.legend(['Raw Data (Nonstationary)'])
plt.subplot(212)
plt.plot(diff_train_data, 'orange')
plt.legend(['Differenced Data (Stationary)'])
plt.show()


fig,ax = plt.subplots(1,2,figsize=(10,5))
fig.suptitle('Differenced Data')
sm.graphics.tsa.plot_acf(diff_train_data.values.squeeze(), lags=30, ax=ax[0])
sm.graphics.tsa.plot_pacf(diff_train_data.values.squeeze(), lags=30, ax=ax[1]);

Estimate Parameters

# ARIMA model fitting
# The (p,d,q) order of the model for the number of AR parameters, differences, and MA parameters to use.

model = ARIMA(train_data.values, order=(1,1,0))
model_fit = model.fit()
model_fit.summary()
SARIMAX Results
Dep. Variable: y No. Observations: 115
Model: ARIMA(1, 1, 0) Log Likelihood -532.268
Date: Sun, 31 Oct 2021 AIC 1068.536
Time: 12:23:06 BIC 1074.008
Sample: 0 HQIC 1070.757
- 115
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.2904 0.089 3.278 0.001 0.117 0.464
sigma2 664.7320 89.253 7.448 0.000 489.800 839.664
Ljung-Box (L1) (Q): 0.32 Jarque-Bera (JB): 3.25
Prob(Q): 0.57 Prob(JB): 0.20
Heteroskedasticity (H): 6.18 Skew: 0.40
Prob(H) (two-sided): 0.00 Kurtosis: 2.79



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

Diagnosis Check - ARIMA

# Parameter search

print('Examples of parameter combinations for Seasonal ARIMA...')
p = range(0, 3)
d = range(1, 2)
q = range(0, 3)
pdq = list(itertools.product(p, d, q))

aic=[]
for i in pdq:
    model = ARIMA(train_data.values, order=(i))
    model_fit = model.fit()
    print(f'ARIMA: {i} >> AIC : {round(model_fit.aic,2)}')
    aic.append(round(model_fit.aic,2))

Examples of parameter combinations for Seasonal ARIMA...
ARIMA: (0, 1, 0) >> AIC : 1076.27
ARIMA: (0, 1, 1) >> AIC : 1063.65
ARIMA: (0, 1, 2) >> AIC : 1060.69
ARIMA: (1, 1, 0) >> AIC : 1068.54
ARIMA: (1, 1, 1) >> AIC : 1058.25
ARIMA: (1, 1, 2) >> AIC : 1057.33
ARIMA: (2, 1, 0) >> AIC : 1065.64
ARIMA: (2, 1, 1) >> AIC : 1058.65
ARIMA: (2, 1, 2) >> AIC : 1057.52

# Search optimal parameters
optimal = [(pdq[i],j) for i,j in enumerate(aic) if j ==min(aic)]
optimal

[((1, 1, 2), 1057.33)]

model_opt = ARIMA(train_data.values, order=optimal[0][0])
model_opt_fit = model_opt.fit()

model_opt_fit.summary()
SARIMAX Results
Dep. Variable: y No. Observations: 115
Model: ARIMA(1, 1, 2) Log Likelihood -524.664
Date: Sun, 31 Oct 2021 AIC 1057.328
Time: 12:23:06 BIC 1068.272
Sample: 0 HQIC 1061.769
- 115
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.5387 0.128 4.219 0.000 0.288 0.789
ma.L1 -0.2053 0.122 -1.688 0.091 -0.444 0.033
ma.L2 -0.5606 0.084 -6.647 0.000 -0.726 -0.395
sigma2 578.5728 105.827 5.467 0.000 371.155 785.991
Ljung-Box (L1) (Q): 0.52 Jarque-Bera (JB): 4.81
Prob(Q): 0.47 Prob(JB): 0.09
Heteroskedasticity (H): 5.54 Skew: 0.18
Prob(H) (two-sided): 0.00 Kurtosis: 2.06



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

Diagnosis check - SARIMA

# parameter search

print('Examples of parameter combinations for Seasoncal ARIMA...')
p = range(0,3)
d = range(1,2)
q = range(0,3)
pdq = list(itertools.product(p,d,q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]

aic=[]
params=[]
for i in pdq:
    for j in seasonal_pdq:
        try:
            model = SARIMAX(train_data.values, order=(i), seasonal_order = (j))
            model_fit = model.fit()
            print(f'SARIMA: {i}{j} >> AIC : {round(model_fit.aic,2)}')
            aic.append(round(model_fit.aic,2))
            params.append((i,j))
        except:
            continue

Examples of parameter combinations for Seasoncal ARIMA...
SARIMA: (0, 1, 0)(0, 1, 0, 12) >> AIC : 757.83
SARIMA: (0, 1, 0)(0, 1, 1, 12) >> AIC : 756.99
SARIMA: (0, 1, 0)(0, 1, 2, 12) >> AIC : 758.83
SARIMA: (0, 1, 0)(1, 1, 0, 12) >> AIC : 756.96
SARIMA: (0, 1, 0)(1, 1, 1, 12) >> AIC : 758.92
SARIMA: (0, 1, 0)(1, 1, 2, 12) >> AIC : 754.42
SARIMA: (0, 1, 0)(2, 1, 0, 12) >> AIC : 758.87
SARIMA: (0, 1, 0)(2, 1, 1, 12) >> AIC : 760.73
SARIMA: (0, 1, 0)(2, 1, 2, 12) >> AIC : 754.89
SARIMA: (0, 1, 1)(0, 1, 0, 12) >> AIC : 756.01
SARIMA: (0, 1, 1)(0, 1, 1, 12) >> AIC : 756.38
SARIMA: (0, 1, 1)(0, 1, 2, 12) >> AIC : 757.65
SARIMA: (0, 1, 1)(1, 1, 0, 12) >> AIC : 756.17
SARIMA: (0, 1, 1)(1, 1, 1, 12) >> AIC : 758.11
SARIMA: (0, 1, 1)(1, 1, 2, 12) >> AIC : 751.73
SARIMA: (0, 1, 1)(2, 1, 0, 12) >> AIC : 757.99
SARIMA: (0, 1, 1)(2, 1, 1, 12) >> AIC : 753.78
SARIMA: (0, 1, 1)(2, 1, 2, 12) >> AIC : 76.48
SARIMA: (0, 1, 2)(0, 1, 0, 12) >> AIC : 757.78
SARIMA: (0, 1, 2)(0, 1, 1, 12) >> AIC : 758.04
SARIMA: (0, 1, 2)(0, 1, 2, 12) >> AIC : 759.28
SARIMA: (0, 1, 2)(1, 1, 0, 12) >> AIC : 757.81
SARIMA: (0, 1, 2)(1, 1, 1, 12) >> AIC : 759.75
SARIMA: (0, 1, 2)(1, 1, 2, 12) >> AIC : 753.5
SARIMA: (0, 1, 2)(2, 1, 0, 12) >> AIC : 759.64
SARIMA: (0, 1, 2)(2, 1, 1, 12) >> AIC : 755.48
SARIMA: (0, 1, 2)(2, 1, 2, 12) >> AIC : 762.02
SARIMA: (1, 1, 0)(0, 1, 0, 12) >> AIC : 755.5
SARIMA: (1, 1, 0)(0, 1, 1, 12) >> AIC : 755.98
SARIMA: (1, 1, 0)(0, 1, 2, 12) >> AIC : 757.1
SARIMA: (1, 1, 0)(1, 1, 0, 12) >> AIC : 755.75
SARIMA: (1, 1, 0)(1, 1, 1, 12) >> AIC : 757.65
SARIMA: (1, 1, 0)(1, 1, 2, 12) >> AIC : 751.15
SARIMA: (1, 1, 0)(2, 1, 0, 12) >> AIC : 757.45
SARIMA: (1, 1, 0)(2, 1, 1, 12) >> AIC : 752.99
SARIMA: (1, 1, 1)(0, 1, 0, 12) >> AIC : 756.02
SARIMA: (1, 1, 1)(0, 1, 1, 12) >> AIC : 756.63
SARIMA: (1, 1, 1)(0, 1, 2, 12) >> AIC : 757.75
SARIMA: (1, 1, 1)(1, 1, 0, 12) >> AIC : 756.41
SARIMA: (1, 1, 1)(1, 1, 1, 12) >> AIC : 758.26
SARIMA: (1, 1, 1)(1, 1, 2, 12) >> AIC : 752.53
SARIMA: (1, 1, 1)(2, 1, 0, 12) >> AIC : 758.03
SARIMA: (1, 1, 1)(2, 1, 1, 12) >> AIC : 754.17
SARIMA: (1, 1, 2)(0, 1, 0, 12) >> AIC : 757.92
SARIMA: (1, 1, 2)(0, 1, 1, 12) >> AIC : 758.44
SARIMA: (1, 1, 2)(0, 1, 2, 12) >> AIC : 759.63
SARIMA: (1, 1, 2)(1, 1, 0, 12) >> AIC : 758.22
SARIMA: (1, 1, 2)(1, 1, 1, 12) >> AIC : 760.1
SARIMA: (1, 1, 2)(1, 1, 2, 12) >> AIC : 754.53
SARIMA: (1, 1, 2)(2, 1, 0, 12) >> AIC : 759.92
SARIMA: (1, 1, 2)(2, 1, 1, 12) >> AIC : 756.16
SARIMA: (2, 1, 0)(0, 1, 0, 12) >> AIC : 756.77
SARIMA: (2, 1, 0)(0, 1, 1, 12) >> AIC : 757.23
SARIMA: (2, 1, 0)(0, 1, 2, 12) >> AIC : 758.31
SARIMA: (2, 1, 0)(1, 1, 0, 12) >> AIC : 756.98
SARIMA: (2, 1, 0)(1, 1, 1, 12) >> AIC : 758.86
SARIMA: (2, 1, 0)(1, 1, 2, 12) >> AIC : 752.77
SARIMA: (2, 1, 0)(2, 1, 0, 12) >> AIC : 758.65
SARIMA: (2, 1, 0)(2, 1, 1, 12) >> AIC : 754.51
SARIMA: (2, 1, 1)(0, 1, 0, 12) >> AIC : 757.98
SARIMA: (2, 1, 1)(0, 1, 1, 12) >> AIC : 758.54
SARIMA: (2, 1, 1)(0, 1, 2, 12) >> AIC : 759.69
SARIMA: (2, 1, 1)(1, 1, 0, 12) >> AIC : 758.31
SARIMA: (2, 1, 1)(1, 1, 1, 12) >> AIC : 760.18
SARIMA: (2, 1, 1)(1, 1, 2, 12) >> AIC : 754.54
SARIMA: (2, 1, 1)(2, 1, 0, 12) >> AIC : 759.98
SARIMA: (2, 1, 1)(2, 1, 1, 12) >> AIC : 756.17
SARIMA: (2, 1, 2)(0, 1, 0, 12) >> AIC : 755.2
SARIMA: (2, 1, 2)(0, 1, 1, 12) >> AIC : 755.99
SARIMA: (2, 1, 2)(0, 1, 2, 12) >> AIC : 759.77
SARIMA: (2, 1, 2)(1, 1, 0, 12) >> AIC : 755.82
SARIMA: (2, 1, 2)(1, 1, 1, 12) >> AIC : 757.71
SARIMA: (2, 1, 2)(1, 1, 2, 12) >> AIC : 752.34
SARIMA: (2, 1, 2)(2, 1, 0, 12) >> AIC : 757.56
SARIMA: (2, 1, 2)(2, 1, 1, 12) >> AIC : 753.96
SARIMA: (2, 1, 2)(2, 1, 2, 12) >> AIC : 761.42

optimal = [(params[i], j) for i,j in enumerate(aic) if j ==min(aic)]
optimal

[(((0, 1, 1), (2, 1, 2, 12)), 76.48)]

model_opt = SARIMAX(train_data.values, order=optimal[0][0][0], seasonal_order = optimal[0][0][1])
model_opt_fit = model.fit()

model_opt_fit.summary()
SARIMAX Results
Dep. Variable: y No. Observations: 115
Model: SARIMAX(2, 1, 2)x(2, 1, 2, 12) Log Likelihood -371.709
Date: Sun, 31 Oct 2021 AIC 761.418
Time: 12:24:20 BIC 785.043
Sample: 0 HQIC 770.984
- 115
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.2347 0.285 0.823 0.411 -0.324 0.794
ar.L2 0.5520 0.240 2.304 0.021 0.082 1.022
ma.L1 -0.5445 0.337 -1.614 0.106 -1.205 0.117
ma.L2 -0.4498 0.311 -1.447 0.148 -1.059 0.160
ar.S.L12 0.0120 0.065 0.185 0.853 -0.115 0.139
ar.S.L24 0.9879 0.127 7.797 0.000 0.740 1.236
ma.S.L12 -0.0374 0.285 -0.132 0.895 -0.595 0.521
ma.S.L24 -0.9604 0.547 -1.755 0.079 -2.033 0.112
sigma2 81.6117 42.138 1.937 0.053 -0.977 164.201
Ljung-Box (L1) (Q): 0.07 Jarque-Bera (JB): 2.52
Prob(Q): 0.80 Prob(JB): 0.28
Heteroskedasticity (H): 1.03 Skew: 0.36
Prob(H) (two-sided): 0.92 Kurtosis: 2.75



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

prediction = model_opt_fit.get_forecast(len(test_data))
predicted_value = prediction.predicted_mean
predicted_lb = prediction.conf_int()[:,0]
predicted_ub = prediction.conf_int()[:,1]
predict_index = list(test_data.index)
r2 = r2_score(test_data, predicted_value)

fig,ax = plt.subplots(figsize=(12,6))
ax.plot(data, label='Passengers')
ax.vlines(['1958-08-01 00:00:00'], 0, 700, linestyle='--', color='r', label='Start of Forecast')
ax.plot(predict_index, predicted_value, label='Prediction')
ax.fill_between(predict_index, predicted_ub, predicted_lb, color='k', alpha=0.1, label='0.95 Prediction Interval')
ax.legend(loc='upper left')
plt.suptitle(f'SARIMA {optimal[0][0][0]}, {optimal[0][0][1]} Prediction Results (r2_score: {round(r2,2)})')
plt.show()

Diagnosis Check - auto_arima

# Parameter search

auto_arima_model = auto_arima(train_data, start_p=1, start_q=1,
                             max_p=3, max_q=3, m=12, seasonal=True,
                              d=1, D=1,
                              max_P=3, max_Q=3,
                              trace=True,
                              error_action='ignore',
                              suppress_warnings=True,
                              stepwise=False                         
                             )

 ARIMA(0,1,0)(0,1,0)[12]             : AIC=757.826, Time=0.01 sec
 ARIMA(0,1,0)(0,1,1)[12]             : AIC=756.988, Time=0.07 sec
 ARIMA(0,1,0)(0,1,2)[12]             : AIC=758.826, Time=0.39 sec
 ARIMA(0,1,0)(0,1,3)[12]             : AIC=758.186, Time=0.64 sec
 ARIMA(0,1,0)(1,1,0)[12]             : AIC=756.959, Time=0.04 sec
 ARIMA(0,1,0)(1,1,1)[12]             : AIC=758.922, Time=0.12 sec
 ARIMA(0,1,0)(1,1,2)[12]             : AIC=inf, Time=1.00 sec
 ARIMA(0,1,0)(1,1,3)[12]             : AIC=754.685, Time=2.00 sec
 ARIMA(0,1,0)(2,1,0)[12]             : AIC=758.869, Time=0.13 sec
 ARIMA(0,1,0)(2,1,1)[12]             : AIC=760.726, Time=0.58 sec
 ARIMA(0,1,0)(2,1,2)[12]             : AIC=inf, Time=1.53 sec
 ARIMA(0,1,0)(2,1,3)[12]             : AIC=756.686, Time=2.51 sec
 ARIMA(0,1,0)(3,1,0)[12]             : AIC=759.643, Time=0.37 sec
 ARIMA(0,1,0)(3,1,1)[12]             : AIC=inf, Time=3.13 sec
 ARIMA(0,1,0)(3,1,2)[12]             : AIC=756.688, Time=3.27 sec
 ARIMA(0,1,1)(0,1,0)[12]             : AIC=756.011, Time=0.02 sec
 ARIMA(0,1,1)(0,1,1)[12]             : AIC=756.380, Time=0.09 sec
 ARIMA(0,1,1)(0,1,2)[12]             : AIC=757.653, Time=0.58 sec
 ARIMA(0,1,1)(0,1,3)[12]             : AIC=756.866, Time=0.84 sec
 ARIMA(0,1,1)(1,1,0)[12]             : AIC=756.166, Time=0.06 sec
 ARIMA(0,1,1)(1,1,1)[12]             : AIC=758.107, Time=0.17 sec
 ARIMA(0,1,1)(1,1,2)[12]             : AIC=inf, Time=1.90 sec
 ARIMA(0,1,1)(1,1,3)[12]             : AIC=752.982, Time=1.73 sec
 ARIMA(0,1,1)(2,1,0)[12]             : AIC=757.994, Time=0.20 sec
 ARIMA(0,1,1)(2,1,1)[12]             : AIC=inf, Time=1.17 sec
 ARIMA(0,1,1)(2,1,2)[12]             : AIC=inf, Time=7.91 sec
 ARIMA(0,1,1)(3,1,0)[12]             : AIC=758.104, Time=0.50 sec
 ARIMA(0,1,1)(3,1,1)[12]             : AIC=inf, Time=3.60 sec
 ARIMA(0,1,2)(0,1,0)[12]             : AIC=757.778, Time=0.03 sec
 ARIMA(0,1,2)(0,1,1)[12]             : AIC=758.043, Time=0.14 sec
 ARIMA(0,1,2)(0,1,2)[12]             : AIC=759.284, Time=0.73 sec
 ARIMA(0,1,2)(0,1,3)[12]             : AIC=758.652, Time=1.05 sec
 ARIMA(0,1,2)(1,1,0)[12]             : AIC=757.811, Time=0.09 sec
 ARIMA(0,1,2)(1,1,1)[12]             : AIC=759.751, Time=0.17 sec
 ARIMA(0,1,2)(1,1,2)[12]             : AIC=inf, Time=2.30 sec
 ARIMA(0,1,2)(2,1,0)[12]             : AIC=759.641, Time=0.26 sec
 ARIMA(0,1,2)(2,1,1)[12]             : AIC=inf, Time=1.87 sec
 ARIMA(0,1,2)(3,1,0)[12]             : AIC=759.804, Time=0.62 sec
 ARIMA(0,1,3)(0,1,0)[12]             : AIC=752.936, Time=0.05 sec
 ARIMA(0,1,3)(0,1,1)[12]             : AIC=753.809, Time=0.17 sec
 ARIMA(0,1,3)(0,1,2)[12]             : AIC=755.269, Time=1.04 sec
 ARIMA(0,1,3)(1,1,0)[12]             : AIC=753.663, Time=0.11 sec
 ARIMA(0,1,3)(1,1,1)[12]             : AIC=755.497, Time=0.41 sec
 ARIMA(0,1,3)(2,1,0)[12]             : AIC=755.384, Time=0.37 sec
 ARIMA(1,1,0)(0,1,0)[12]             : AIC=755.499, Time=0.02 sec
 ARIMA(1,1,0)(0,1,1)[12]             : AIC=755.982, Time=0.09 sec
 ARIMA(1,1,0)(0,1,2)[12]             : AIC=757.103, Time=0.54 sec
 ARIMA(1,1,0)(0,1,3)[12]             : AIC=756.433, Time=0.74 sec
 ARIMA(1,1,0)(1,1,0)[12]             : AIC=755.750, Time=0.06 sec
 ARIMA(1,1,0)(1,1,1)[12]             : AIC=757.649, Time=0.14 sec
 ARIMA(1,1,0)(1,1,2)[12]             : AIC=inf, Time=1.47 sec
 ARIMA(1,1,0)(1,1,3)[12]             : AIC=752.557, Time=1.93 sec
 ARIMA(1,1,0)(2,1,0)[12]             : AIC=757.453, Time=0.19 sec
 ARIMA(1,1,0)(2,1,1)[12]             : AIC=inf, Time=1.30 sec
 ARIMA(1,1,0)(2,1,2)[12]             : AIC=inf, Time=nan sec
 ARIMA(1,1,0)(3,1,0)[12]             : AIC=757.510, Time=0.49 sec
 ARIMA(1,1,0)(3,1,1)[12]             : AIC=inf, Time=3.77 sec
 ARIMA(1,1,1)(0,1,0)[12]             : AIC=756.022, Time=0.04 sec
 ARIMA(1,1,1)(0,1,1)[12]             : AIC=756.629, Time=0.16 sec
 ARIMA(1,1,1)(0,1,2)[12]             : AIC=757.749, Time=0.97 sec
 ARIMA(1,1,1)(0,1,3)[12]             : AIC=757.733, Time=1.54 sec
 ARIMA(1,1,1)(1,1,0)[12]             : AIC=756.406, Time=0.12 sec
 ARIMA(1,1,1)(1,1,1)[12]             : AIC=758.260, Time=0.33 sec
 ARIMA(1,1,1)(1,1,2)[12]             : AIC=inf, Time=1.92 sec
 ARIMA(1,1,1)(2,1,0)[12]             : AIC=758.031, Time=0.35 sec
 ARIMA(1,1,1)(2,1,1)[12]             : AIC=inf, Time=1.63 sec
 ARIMA(1,1,1)(3,1,0)[12]             : AIC=758.462, Time=0.94 sec
 ARIMA(1,1,2)(0,1,0)[12]             : AIC=757.925, Time=0.04 sec
 ARIMA(1,1,2)(0,1,1)[12]             : AIC=758.441, Time=0.21 sec
 ARIMA(1,1,2)(0,1,2)[12]             : AIC=759.634, Time=1.02 sec
 ARIMA(1,1,2)(1,1,0)[12]             : AIC=758.220, Time=0.14 sec
 ARIMA(1,1,2)(1,1,1)[12]             : AIC=760.100, Time=0.36 sec
 ARIMA(1,1,2)(2,1,0)[12]             : AIC=759.915, Time=0.40 sec
 ARIMA(1,1,3)(0,1,0)[12]             : AIC=754.178, Time=0.10 sec
 ARIMA(1,1,3)(0,1,1)[12]             : AIC=753.995, Time=0.48 sec
 ARIMA(1,1,3)(1,1,0)[12]             : AIC=753.975, Time=0.41 sec
 ARIMA(2,1,0)(0,1,0)[12]             : AIC=756.771, Time=0.03 sec
 ARIMA(2,1,0)(0,1,1)[12]             : AIC=757.226, Time=0.12 sec
 ARIMA(2,1,0)(0,1,2)[12]             : AIC=758.313, Time=0.68 sec
 ARIMA(2,1,0)(0,1,3)[12]             : AIC=758.011, Time=0.90 sec
 ARIMA(2,1,0)(1,1,0)[12]             : AIC=756.982, Time=0.09 sec
 ARIMA(2,1,0)(1,1,1)[12]             : AIC=758.859, Time=0.23 sec
 ARIMA(2,1,0)(1,1,2)[12]             : AIC=inf, Time=1.86 sec
 ARIMA(2,1,0)(2,1,0)[12]             : AIC=758.650, Time=0.27 sec
 ARIMA(2,1,0)(2,1,1)[12]             : AIC=inf, Time=1.90 sec
 ARIMA(2,1,0)(3,1,0)[12]             : AIC=758.903, Time=0.61 sec
 ARIMA(2,1,1)(0,1,0)[12]             : AIC=757.976, Time=0.05 sec
 ARIMA(2,1,1)(0,1,1)[12]             : AIC=758.537, Time=0.27 sec
 ARIMA(2,1,1)(0,1,2)[12]             : AIC=759.694, Time=1.11 sec
 ARIMA(2,1,1)(1,1,0)[12]             : AIC=758.314, Time=0.16 sec
 ARIMA(2,1,1)(1,1,1)[12]             : AIC=760.183, Time=0.35 sec
 ARIMA(2,1,1)(2,1,0)[12]             : AIC=759.976, Time=0.49 sec
 ARIMA(2,1,2)(0,1,0)[12]             : AIC=755.201, Time=0.14 sec
 ARIMA(2,1,2)(0,1,1)[12]             : AIC=755.987, Time=0.39 sec
 ARIMA(2,1,2)(1,1,0)[12]             : AIC=755.821, Time=0.43 sec
 ARIMA(2,1,3)(0,1,0)[12]             : AIC=755.253, Time=0.31 sec
 ARIMA(3,1,0)(0,1,0)[12]             : AIC=755.605, Time=0.04 sec
 ARIMA(3,1,0)(0,1,1)[12]             : AIC=756.424, Time=0.14 sec
 ARIMA(3,1,0)(0,1,2)[12]             : AIC=757.829, Time=0.83 sec
 ARIMA(3,1,0)(1,1,0)[12]             : AIC=756.268, Time=0.11 sec
 ARIMA(3,1,0)(1,1,1)[12]             : AIC=758.159, Time=0.28 sec
 ARIMA(3,1,0)(2,1,0)[12]             : AIC=758.003, Time=0.31 sec
 ARIMA(3,1,1)(0,1,0)[12]             : AIC=754.435, Time=0.12 sec
 ARIMA(3,1,1)(0,1,1)[12]             : AIC=754.694, Time=0.38 sec
 ARIMA(3,1,1)(1,1,0)[12]             : AIC=754.571, Time=0.36 sec
 ARIMA(3,1,2)(0,1,0)[12]             : AIC=inf, Time=0.33 sec

Best model:  ARIMA(1,1,0)(1,1,3)[12]          
Total fit time: 82.425 seconds

auto_arima_model.summary()
SARIMAX Results
Dep. Variable: y No. Observations: 115
Model: SARIMAX(1, 1, 0)x(1, 1, [1, 2, 3], 12) Log Likelihood -370.278
Date: Sun, 31 Oct 2021 AIC 752.557
Time: 12:25:42 BIC 768.307
Sample: 0 HQIC 758.934
- 115
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 -0.2218 0.093 -2.388 0.017 -0.404 -0.040
ar.S.L12 0.9288 0.275 3.374 0.001 0.389 1.468
ma.S.L12 -1.2065 0.448 -2.692 0.007 -2.085 -0.328
ma.S.L24 0.2771 0.174 1.596 0.111 -0.063 0.618
ma.S.L36 0.1251 0.164 0.765 0.444 -0.195 0.446
sigma2 75.0386 19.073 3.934 0.000 37.656 112.421
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 2.50
Prob(Q): 0.91 Prob(JB): 0.29
Heteroskedasticity (H): 1.05 Skew: 0.37
Prob(H) (two-sided): 0.90 Kurtosis: 2.81



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

prediction = auto_arima_model.predict(len(test_data), return_conf_int=True)
predicted_value = prediction[0]
predicted_lb = prediction[1][:,0]
predicted_ub = prediction[1][:,1]
predict_index = list(test_data.index)
r2 = r2_score(test_data, predicted_value)

fig,ax = plt.subplots(figsize=(12,6))
ax.plot(data, label='Passengers')
ax.vlines(['1958-08-01 00:00:00'], 0, 700, linestyle='--', color='r', label='Start of Forecast')
ax.plot(predict_index, predicted_value, label='Prediction')
ax.fill_between(predict_index, predicted_ub, predicted_lb, color='k', alpha=0.1, label='0.95 Prediction Interval')
ax.legend(loc='upper left')
plt.suptitle(f'SARIMA {optimal[0][0][0]}, {optimal[0][0][1]} Prediction Results (r2_score: {round(r2,2)})')
plt.show()

adfuller 사용하여 Stationary 판별

from statsmodels.tsa.stattools import adfuller

res = sm.tsa.adfuller(train_data.dropna(),regression='ct')
print('p-value:{}'.format(res[1]))

p-value:0.46898818429932104

res = sm.tsa.adfuller(train_data.diff().dropna(),regression='c')
print('p-value:{}'.format(res[1]))

p-value:0.10612609999673356

def print_adfuller(inputseries):
    result= adfuller(inputseries)
    print('ADF Statisic: %f' % result[0])
    print('p-value: %f' % result[1])
    print('Critical Values:')
    for key, value in result[4].items():
        print('\t%s: %.3f' % (key, value))

print_adfuller(train_data.diff().dropna())

ADF Statisic: -2.539635
p-value: 0.106126
Critical Values:
	1%: -3.498
	5%: -2.891
	10%: -2.582
  • 검정통계량(ADF Statistics) 가 Critical Vlaue보다 작거나 P-value가 설정한 신뢰수준 값(0.05) 보다 작으면 Stationary한 시계열 데이터
res = sm.tsa.arma_order_select_ic(train_data.diff(), max_ar=3, max_ma=3, ic='aic', trend='c')
print('ARMA(p,q) =',res['aic_min_order'],'is the best.')

ARMA(p,q) = (3, 3) is the best.

ARIMA Model

arima = sm.tsa.statespace.SARIMAX(train_data,order=(3,1,3),seasonal_order=(0,0,0,0),
                                 enforce_stationarity=False, enforce_invertibility=False,).fit()
arima.summary()
SARIMAX Results
Dep. Variable: passengers No. Observations: 115
Model: SARIMAX(3, 1, 3) Log Likelihood -490.741
Date: Sun, 31 Oct 2021 AIC 995.483
Time: 12:25:45 BIC 1014.386
Sample: 01-01-1949 HQIC 1003.150
- 07-01-1958
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 1.0207 0.116 8.782 0.000 0.793 1.249
ar.L2 0.1890 0.180 1.049 0.294 -0.164 0.542
ar.L3 -0.6282 0.112 -5.616 0.000 -0.847 -0.409
ma.L1 -0.8570 137.320 -0.006 0.995 -270.000 268.286
ma.L2 -0.9664 2.436 -0.397 0.692 -5.742 3.809
ma.L3 1.0378 150.417 0.007 0.994 -293.774 295.849
sigma2 375.2869 5.44e+04 0.007 0.994 -1.06e+05 1.07e+05
Ljung-Box (L1) (Q): 0.97 Jarque-Bera (JB): 1.35
Prob(Q): 0.32 Prob(JB): 0.51
Heteroskedasticity (H): 3.99 Skew: 0.23
Prob(H) (two-sided): 0.00 Kurtosis: 2.70



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

res = arima.resid
fig,ax = plt.subplots(2,1,figsize=(15,8))
fig = sm.graphics.tsa.plot_acf(res, lags=50, ax=ax[0])
fig = sm.graphics.tsa.plot_pacf(res, lags=50, ax=ax[1])
plt.show()


tr_start,tr_end = '1949-01-01','1958-07-01'
te_start,te_end = '1958-08-01','1960-12-01'

from sklearn.metrics import mean_squared_error
pred = arima.predict(tr_end,te_end)[1:]
print('ARIMA model MSE:{}'.format(mean_squared_error(test_data['passengers'],pred)))

ARIMA model MSE:4957.217448681122

pd.DataFrame({'test':test_data['passengers'],'pred':pred}).plot();plt.show()

SARIMA MODEL

sarima = sm.tsa.statespace.SARIMAX(train_data,
                                   order=(2,0,3),
                                   seasonal_order=(2,0,3,12),
                                enforce_stationarity=False, enforce_invertibility=False).fit()
sarima.summary()
SARIMAX Results
Dep. Variable: passengers No. Observations: 115
Model: SARIMAX(2, 0, 3)x(2, 0, 3, 12) Log Likelihood -265.269
Date: Sun, 31 Oct 2021 AIC 552.539
Time: 12:25:48 BIC 578.031
Sample: 01-01-1949 HQIC 562.717
- 07-01-1958
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.3423 0.871 0.393 0.694 -1.365 2.050
ar.L2 0.2086 0.658 0.317 0.751 -1.081 1.498
ma.L1 0.4038 0.866 0.466 0.641 -1.294 2.101
ma.L2 0.3999 0.194 2.064 0.039 0.020 0.780
ma.L3 0.1854 0.309 0.601 0.548 -0.419 0.790
ar.S.L12 0.4910 0.090 5.446 0.000 0.314 0.668
ar.S.L24 0.7204 0.104 6.950 0.000 0.517 0.924
ma.S.L12 0.0616 0.563 0.109 0.913 -1.042 1.165
ma.S.L24 -1.0491 0.479 -2.189 0.029 -1.989 -0.110
ma.S.L36 -0.4966 0.261 -1.902 0.057 -1.008 0.015
sigma2 40.7933 22.731 1.795 0.073 -3.759 85.346
Ljung-Box (L1) (Q): 0.03 Jarque-Bera (JB): 0.87
Prob(Q): 0.87 Prob(JB): 0.65
Heteroskedasticity (H): 0.67 Skew: -0.19
Prob(H) (two-sided): 0.32 Kurtosis: 2.64



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

res = sarima.resid
fig,ax = plt.subplots(2,1,figsize=(15,8))
fig = sm.graphics.tsa.plot_acf(res, lags=50, ax=ax[0])
fig = sm.graphics.tsa.plot_pacf(res, lags=50, ax=ax[1])
plt.show()


from sklearn.metrics import mean_squared_error
pred = sarima.predict(tr_end,te_end)[1:]
print('ARIMA model MSE:{}'.format(mean_squared_error(test_data['passengers'],pred)))

ARIMA model MSE:837.0432041535151

pd.DataFrame({'test':test_data['passengers'],'pred':pred}).plot();plt.show()

출처1 -

유투브 인공지능공학연구소 김성범 소장님 강의

출처2 -
Kaggle How to use SARIMAX

댓글남기기

참고

ChatGPT를 위한 최적의 프롬프트 만들기

AI 언어 모델인 ChatGPT와 같은 모델이 인기를 얻으면서 AI와 효과적으로 상호 작용하는 것이 점점 중요해지고 있습니다. ChatGPT에서 가장 정확하고 유용한 결과를 얻으려면 신중하게 고안된 프롬프트를 사용해야 합니다. 이 게시물에서는 ChatGPT를 위한 이상적인 프롬프트...

Crafting the Ultimate Prompts for ChatGPT

As AI language models like ChatGPT continue gaining popularity, effectively interacting with them has become increasingly important. To get the most accurate...

머신러닝 vs 딥러닝

머신 러닝과 딥 러닝은 인공 지능(AI) 분야에서 두 가지 중요한 개념입니다. 종종 서로 바꿔 사용되지만, 두 개념의 원리와 차이점을 이해하는 것이 중요합니다. 이 글에서는 머신 러닝과 딥 러닝의 핵심 아이디어, 강점 및 약점을 탐구하여 둘의 차이점을 완전히 이해해보겠습니다.