CS231n_Lecture 3 (1/2)

Loss Functions and Optimization (1/2)

---

Loss Functions

Linear Classifier

• 지난 강의에서 Linear classifier(선형 분류기)의 아이디어에 대해서 이야기 하였고 이번 강의에서는 어떤 W가 Class를 분류하기에 좋은 W 값이고 어떤 W가 안좋은 값인지 어떻게 분류하는지 알아보려함.
• 예를 들면 고양이 이미지에서 W 값을 보면 고양이 Class에 2.9점을 주었고 개구리 Class에는 3.78점을 주었음.
• 이는 Classifier (분류기)가 잘 작동하지 않는다고 볼 수 있음.
• 자동차 이미지의 경우는 자동차 Class에 가장 높은 점수를 주었기 때문에 좋은 분류기라 할 수 있음.
• 하지만 단순히 높은 W 점수를 찾는 것은 논리가 부족한 접근 방식이고 W의 좋고 나쁨 정도를 정량화 할 수 있는 방법이 필요함.

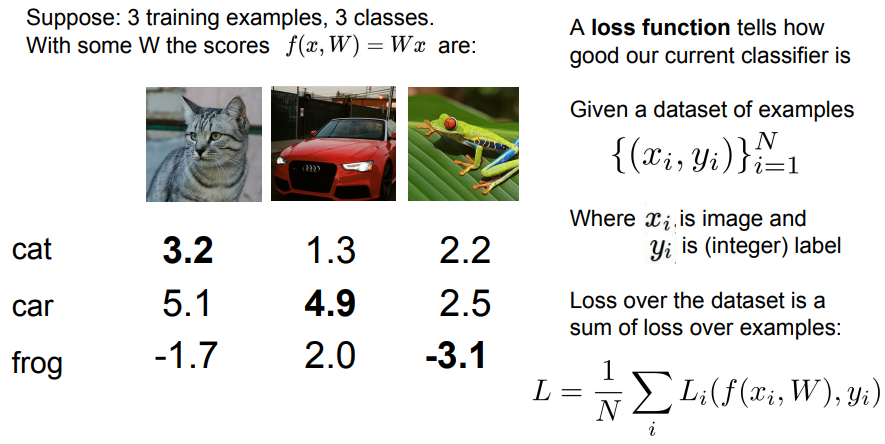
• 앞선 예시를 3개의 Class로 줄여서 보면 고양이 이미지는 잘 분류되지 않았고, 자동차는 자동차 Class가 점수가 가장 높았으므로 잘 분류 한 것으로 보임.
• Loss function은 Classifier의 성능이 얼마나 좋은지를 알려주는 역할을 하고 Li로 표시함.
• Lossfunction은 Input Image “x”와 Weight matrix “W”를 받은 함수 예측함수 f 가 예측한 값과 실제 Label인 “y” 값과의 비교를 통해 정의됨.
• 최종적으로 Loss function은 Dataset N개에 걸쳐 전체 Dataset을 합친것에 대한 Loss들의 평균임.

Multiclass SVM Loss

• Loss function의 예로 이미지 분류가 잘되는 Multiclass SVM(Support Vector Machine) 를 살펴봄 (이진 분류에 사용되는 Binary SVM을 일반화한 형태)
• SVM의 Loss function 에서는 잘못된 Label score( j ≠ yi)인 경우에만 Loss를 계산함.
• 정답 Category(Syi)의 점수와 오답 Category(Sj)의 점수를 비교하여 $(Syi - Sj)$ 설정된 Safety margin (이 예제에서는 Safety margin이 1 )보다 크면 Loss는 0이되고 , 그 이외의 경우에는 $Sj - Syi$ 값에 Safety margin을 더해서 Loss를 구해줌.
• 이를 Max 함수로 간략화 시키면 $max(0, Sj - Syi +1)$ 와 같음.

Support Vector Machine

• 만약 Class를 올바르게 경우가 많아지면, Safety margin 까지 Loss는 선형으로 줄어들다가 Safety margin 이후에는 Loss가 0이됨.
• 이런 형식의 Loss function을 Hinge Loss라 부름. (그래프의 모양이 지렛대와 비슷하게 생겨서 Hinge Loss)

• 각 Class 들에 대하여 SVM Loss를 순서대로 계산해 봄.
• 고양이의 경우 첫 번째 값 3.2는 정답 Class의 값이므로 계산하지 않고, 자동차 점수는 고양이 점수 보다 높으므로, 자동차 점수에서 고양이 점수를 빼고 Safety margin을 더해줌. (5.1-3.2+1=2.9)
• 개구리 점수는 -1.7로 고양이 점수 3.2보다 작으므로 Loss는 0이 됨.
• Loss의 합은 2.9 + 0 = 2.9 이고 해당 값이 Classifier의 성능을 평가할 수 있는 정량적 측정 값임.

• 자동차 Class에 대해서도 동일하게 계산. (Loss의 합은 0)

• 개구리 Class에 대해서도 계산. (Loss의 합은 12.9)

• 전체 Dataset에 대한 Classifier의 성능은 모든 Class Loss의 평균임.
• 따라서, L = 5.27 이고 예시의 Classifier가 해당 Dataset에 대해서 5.27만큼 성능이 좋지 않다는 것을 의미함. (L값이 실제 값에 대한 Loss 값이므로 0에 가까울 수록 분류를 잘 한것.)
• Q1 : 만약 자동차 이미지를 조금 바꾼다면 Loss에 영향이 생길까?
  • SVM Loss는 정답 Class의 점수가 오답 Class의 점수보다 Safety margin 보다 더 큰지에 관심이 있고, 자동차 Class의 점수가 충분히 크다면 자동차 이미지가 바뀌어도 손실은 여전히 0임.
• Q2: Loss의 최소/최대값은?
  • 최소 Loss는 0이고 최대 Loss는 무한대,
• Q3: Initialization(초기화) 시 W가 너무 작아서 모든 s가 0에 가깝다면 Loss 는?
  • Class의 점수가 0에 가깝다면 Loss는 Safety margin과 동일하게 될 것임.(이 예제에서는 1, 전체 Loss는 Class 수 -1, 각 Class 계산 마다 Safety margin이 있으므로 )
  • 이는 Debugging 전략으로도 쓰이는데 초기 Score 값을 매우 작게 시작했을때 초기 Loss가 (Class 수 -1)* Safety margin 이 아니면 bug가 있다는 것을 의미. (Sanity check)
• Q4: 모든 Class(정답 Class포함)에 대해 SVM Loss를 계산하면?
  • 정답 Class의 Loss 값은 Safety margin 값이므로, 최종 Loss도 Safety margin 만큼 증가
• Q5: Loss의 합을 구하지 않고 평균을 구한다면?
  • Loss 값의 크기를 비교하는 것일 뿐이기에 평균을 사용해도 Scale만 변할 뿐임.
• Q6: $Σmax(0, Sj - Syi +1 )^2$ 을 사용 한다면?
  • 제곱을 하면 Loss Function이 비선형적으로 바뀌기 때문에 전혀 다른 Loss fucntion이됨.

  

• Numpy를 사용한 Sample Code

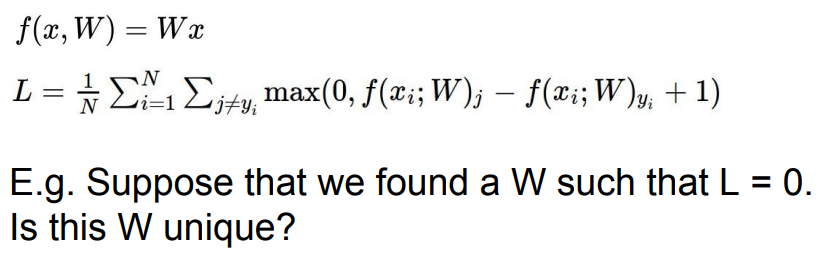
• 만약 Loss=0인 W를 찾았다면, 해당 W는 유일한 W인지?

• 2W의 경우에도 L=0이므로, 유일한 값이 아님.
• L=0을 만족하는 다른 W도 있을 수 있음.

• 한 예로 자동차 Class의 W에 x2를 해서 Loss를 구했을 때, 곱하기 전과 마찬가지로 Loss가 0인 것을 볼 수 있음.

• Model을 만드는 이유는 새로운 값에 대해서 예측을 하기 위함임.
• 지금까지 모델은 Train data에 맞추게 했고 해당 모델이 Train data를 잘 맞추어도 Test set에서는 안맞을 수가 있음.

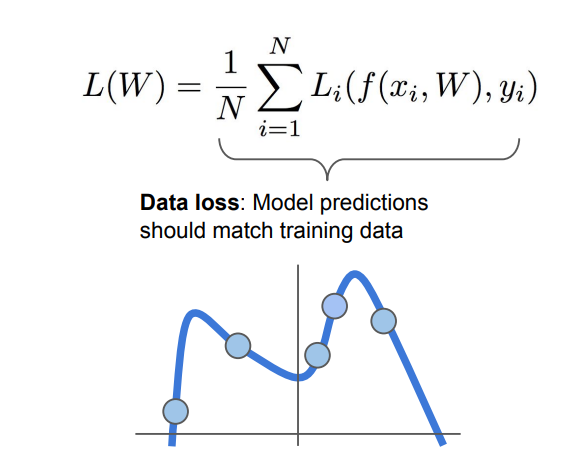
• 파란 점들이 Train data set이라고 했을때 학습데이터 맞는 어떤 곡선을 모델은 그릴것임.
• Train data set을 완벽하게 분류하기 위해 매우 구불구불한 곡선을 가지게 될 것임.

• 만약 새로운 트랜드를 따르는 Data(녹색 네모)와 같은 데이터가 들어오면 예측은 완전히 틀리게 됨.
• Training data에만 맞는 복잡한 곡선 형태로 학습이된 상태를 Overfitting(과적합) 이라함.

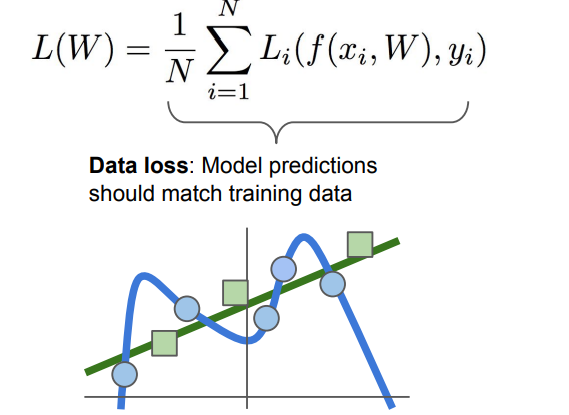
• Training data에 완벽히 맞는 복잡한 곡선 보다 초록색 직선을 예측하는 것이 더 좋은 결과를 가져옴.

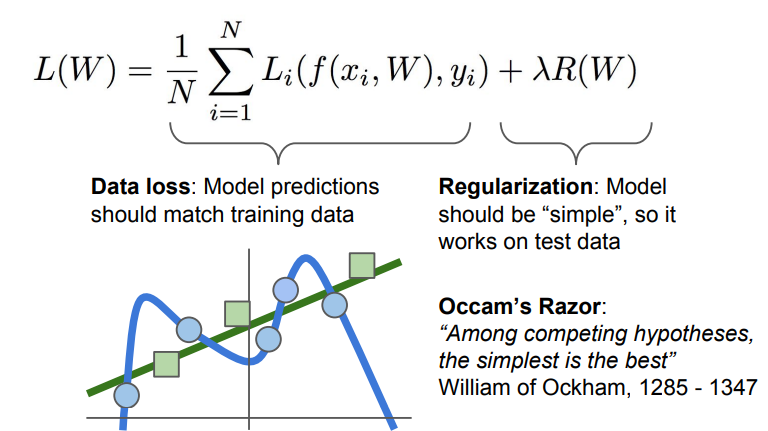
• Test data에도 맞는 W값을 찾으려면 기존 Loss function에 추가적인 항에 Reguralization(정규화) 항을 더해 모델을 단순화 시켜야 함.
• “경쟁을 하는 여러 가설들이 있다면, 간단한 것이 최고”, (Occam’s Razor라는 과학적 이론)

• Raguralization은 여러종류가 있으며, 가장 많이 쓰이는 것은 L2 regularizaion임.

• 예시 데이터 x가 있고 두개의 Weight, W1과 W2가 있을 때, x와 W의 내적을 구하면, 두개의 W는 1로 같음.
  • $w^T_1 x = 1 + 0 + 0 + 0 =1$
  • $w^T_2x = 0.25 + 0.25 + 0.25 + 0.25$
• 첫번째 예는 L1 Regularizaion이 더 선호하며 L1 Regularization은 Weight 벡터에서 0의 갯수로 복잡도를 측정.
• 두번째 예는 L2 Regularizaion이 더 선호하며 L2 Regularizaion은 x의 모든 값에 영향을 끼치고 숫자가 넓게 퍼질 때 모델 복잡도가 덜 복잡해짐.
• L1 Regularizaion은 특성이 일부 제거 되고 L2 Regularizaion은 모든 것을 고려하기 때문에 일반적으로 L1보다 L2가 더 많이 쓰임.

Softmax Classifier (Multinomial Logistic Regression)

• SVM 이외에 딥러닝에서 많이쓰는 Classifier는 Multinomial Logistic Regression임
• SVM에서는 각 Class score에 대한 해석을 하지 않지만, Multinomial Logistic Regression에서는 Class score에 추가적인 의미를 부여함.
• Softmax라고 불리는 함수를 써서 각 항의 점수를 지수화하고 정규화하면 확률 분포를 얻게됨.
• 확률은 0부터 1사이의 수이며, Softmax를 통해 나온 모든 값의 합은 1이됨.

• 만약 Classifier가 고양이라는 것을 확실하게 분류한다면, 고양이의 확률을 1이라고 얻을 것이고 다른 Class는 모두 0이 될것임.

• Softmax function으로 부터 Loss를 정의할때 - log를 취해주면 확률이 0에 가까울 수록 Loss는 발산하고, 1에 가까울 수록 0에 수렴하게 됨.

  

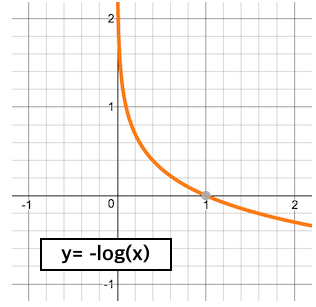
• Class score를 지수화하고 정규화하여 확률로 구한 후 -log를 취해 Loss를 구해봄.
• Q1 : 가능한 Loss의 최대/최소 값은?
  • 최소 손실은 0이고, 최대 손실은 무한대.
    • 정답일경우 확률 x= 1, $Loss = -log(1) = 0$
    • 정답일 확률이 매우 낮을 경우 x = $1/∞$, $Loss = -log(1/∞) = ∞$
• Q2 : Initialization에서 W가 매우 작아 모든 Score가 0이면 Loss는 얼마인가?
  • $Loss = -log(1/C) = log(C)$ (C는 Class 개수)
  • Debug 전략으로 사용(Sanity check)

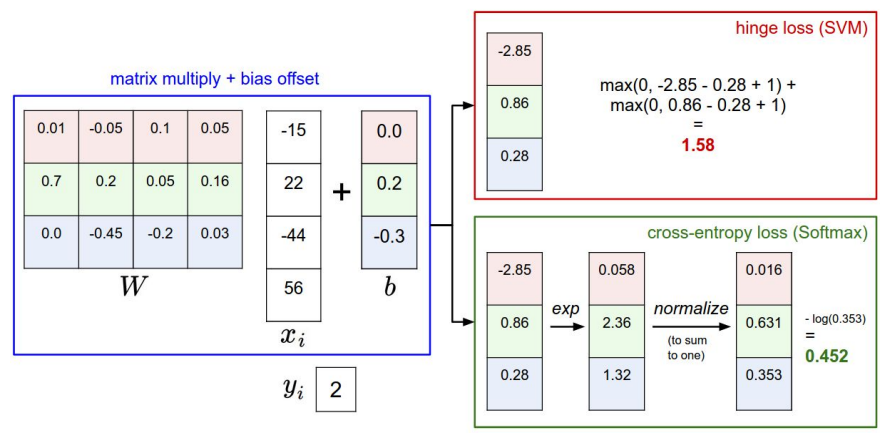
• Hinge loss (SVM)와 Cross-entropy loss(Softmax)를 비교 대조해 보면, 두 Loss 모두 입력에 대해 W를 곱하여 Score를 계산하고 이를 통해 Loss를 계산하는 것은 동일.
• 다만 두 Loss function은 서로 해석하는 방법이 다름.
• SVM은 Class score간의 차이를 통해 Loss를 계산하고 Softmax는 확률 분포를 이용하여 음의 로그 값을 구함.

• SVM에서 자동차 이미지에 약간의 변화를 주어도 다른 Class보다 자동차 Class의 Score가 훨씬 높았기 때문에 변화가 없었음.
• 하지만 Softmax에서는 정답 Class의 예측 점수를 확률로 만들기 때문에 Loss가 변함.

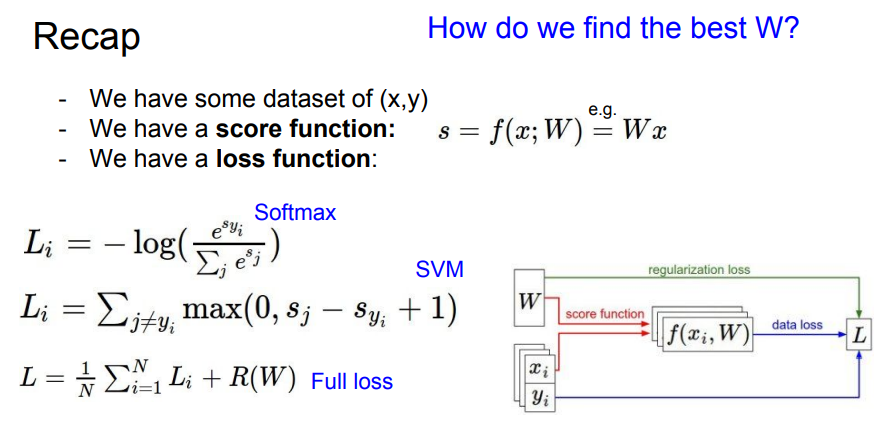
• 지금까지 내용을 정리해보면, Dataset을 Classifier를 통해 Score를 계산하고 Score를 통해 Loss 계산하여 Classifier의 성능을 정량적으로 정의함.
• 결국 Loss를 최소화하는 W를 찾는 것이 중요하고 Loss를 최소화는 W를 찾는 과정이 Optimization (최적화) 임.

---

• 출처

Stanford University Youtube CS231n_Lecture3_1